1 - Introduction
Notion de probabilité
Le calcul des probabilités consiste à mesurer l’apparition ou la non-apparition de certains événements. Il a une importance fondamentale dans tous les problèmes de prévision : jeux de hasard, assurances, météorologie, recherche opérationnelle, pronostics électoraux, mécanique ondulatoire, création de nouveaux produits, etc.
Par exemple, si l’on jette un dé, il n’est pas possible de prédire à coup sûr que le dé va tomber sur le 6. Par contre, intuitivement, on pressent qu’il y a une chance sur 6 pour que le dé tombe sur 6.
Pour ce faire, nous avons supposé que chaque position du dé avait la même chance de succès (on dit que les positions sont équiprobables) et que puisqu’il y a 6 faces à un dé, il y a 1 chance sur 6 que le 6, ou un autre chiffre sorte.
On évalue la probabilité qu’une condition se réalise en divisant le nombre de cas qui sont favorables à cette condition par le nombre de cas total. cette probabilité s’exprime par un nombre toujours compris entre 0 et 1.
- 0 correspond à une probabilité nulle (celle par exemple qu’un dé normal tombe sur un 7),
- 1 correspond à une probabilité de 100 % (celle par exemple qu’un dé normal tombe sur un chiffre compris entre 1 et 6).
Evénements dépendants ou indépendants
On considère que deux événements sont indépendants lorsque la réalisation de l’un n’affecte en rien la probabilité de réalisation de l’autre.
Par exemple, résultats successivement obtenus en jetant un dé. A chaque nouveau jet, les paris restent ouverts avec la même probabilité qu’avant le jet précédent.
A l’inverse, il existe des événements dont la réalisation affecte la probabilité des autres événements.
Supposons que l’on tire successivement des cartes dans un jeu de 32 cartes sans remettre les cartes en place après chaque tirage. Quelle est la probabilité que l’on tire le roi de coeur au premier tirage ? C’est 1/32. Si ce roi n’a pas été tiré, quelle est la probabilité qu’on le tire au deuxième tirage ? Cela n’est plus 1/32, mais 1/31, etc …
On parle de probabilité conditionnelle quand on évalue la probabilité d’un événement E2 sachant que E1 s’est réalisé.
Probabilités composées
Les probabilités composées permettent d’évaluer la probabilité d’une combinaison d’événements dont on connait individuellement les probabilités.
Cas d’événements indépendants
La probabilité qu’un événement E1 se produise et qu’en même temps l’événement E2 se produise aussi est égale au produit des probabilités de chacun des événements.
Supposons que l’on dispose de deux jeux de 32 cartes, l’un vert l’autre jaune. On les mélange en les brassant. Quelle est la probabilité de tirer le roi de coeur vert ?
Probabilité de tirer un roi de coeur = 2 rois de coeur / 64 cartes = 1/32
Probabilité de tirer une carte verte = 32 cartes vertes /64 cartes = 1/2
Probabilité de tirer le roi de coeur vert = 1/32 x 1/2 = 1/64
On vérifie qu’en divisant le nombre de cas favorables (un seul roi de coeur vert) par le nombre de cas possibles (64 cartes) on trouve également 1/64.
Cas d’événements dépendants
La probabilité qu’un événement E1 et E2 indépendants se produisent ensemble est égal à la probabilité que E1 se produise multipliée par la probabilité conditionnelle que E2 se produise après que E1 se soit produit.
Par exemple, je dispose dans une urne d’un lot de 2 boules rouges et 4 boules noires. Si les tirages se font sans remettre les boules dans l’urne, quelle est la probabilité que je tire les 2 boules rouges d’emblée ?
Lors du premier tirage, la probabilité de tirer une boule rouge est de : 2/6 = 1/3. Si j’ai bien tiré une boule rouge, la probabilité de tirer une autre boule rouge au second tirage est de : 1/5 puisqu’il n’y a plus qu’une boule rouge et 4 boules noires dans l’urne.
La probabilité de tirer successivement 2 boules rouges est donc de : 1/3 x 1/5 = 1/15.
Probabilités totales
Etant donné les probabilités de réalisation des événements E1 et E2, la probabilité que l’un des deux événements se produise est égale à la somme des probabilités individuelles de ces événements.
Par exemple, la probabilité qu’un jet de dé donne un résultat pair est égal à la somme des probabilités d’obtenir un 2, un 4 ou un 6.
Ppair = 1/6 + 1/6 + 1/6 = 1/2
Quelques exemples pratiques
Exemple 1 – Sauriez-vous calculer la probabilité de gagner au loto avec les 6 numéros ?
Rappelons qu’il y a 49 numéros dans l’urne du loto.
Au premier tirage, la probabilité que vous ayez un bon numéro est de : 6 / 49.
Au deuxième tirage, la probabilité d’avoir à nouveau un bon numéro est de : 5 / 48 (5 parce qu’il ne me reste que 5 numéros en jeu, et 48 parce qu’il ne reste plus que 48 boules dans l’urne.
Au troisième tirage, la probabilité d’avoir un bon numéro est de : 4 / 47.
Ainsi on obtient les probabilités suivantes : 6/49, 5/48, 4/47, 3/46, 2/45 et 1/44.
La probabilité composée est le produit de ces 6 probabilités individuelles soit :
P = (6 x 5 X 4 x 3 x 2 x 1) / (49 x 48 x 47 x 46 x 45 x 44) = 1 / 13 983 816
C’est donc bien une chance sur 14 millions !
Si vous êtes intéressé par tout ce qui tourne autour des probabilités autour du loto, consultez le site personnel suivant :
http://perso.wanadoo.fr/cyberscargo…
Ce calcul un peu laborieux est formalisé par ce qu’on appelle l’analyse combinatoire qui permet de dénombrer le nombre de combinaisons d’objets.
Soit un lot de n objets distincts et repérables. Combien existe t’il de
combinaisons différentes d’objets pris p par p.
Ce nombre est donné par la formule de combinaison de p parmi n :
Cpn ) = n ! / p ! x (n -p) !
avec n ! = 1 x 2 x 3 x 4 x … x (n-1) x n
Attention : les combinaisons s’entendent sans tenir compte de l’ordre des p éléments (la combinaison 1, 2, 3, 4 est la même que la combinaison 2, 1, 3, 4).
Dans notre calcul précédent , il s’agissait de calculer le nombre de combinaisons de 6 chiffres parmi 49 chiffres sans tenir compte de l’ordre dans lequel les boules tombent.
Si l’on a joué une seule combinaison de 6 chiffres, la probabilité d’avoir la bonne est de 1 divisé par le nombre de combinaisons, soit :
C649 ) = 49 ! / 6 ! x (49 -6) ! = 49 ! / 6 ! x 43 !
C649 ) = 49 x 48 x x 43 x 42 x 41 x … x 3 x 2 x 1) / (6 x 5 x 4 x 3 x 2 x 1 ) x (43 x 42 x … x 3 x 2 x 1)
Soit en simplifiant :
C649 ) = (49 x 48 x 47 x 46 x 45 x 44) / (6 x 5 x 4 x 3 x 2 x 1 ) = 13 983 816.
Exemple 2 : le jeu de 421
Quelle est la probabilité de gagner au 421 en 3 jets de dés ?
ATTENTION : Il s’agit de gagner en 3 jets de dés exactement et donc de n’obtenir 421 qu’au 3 ème jet (soit ni au premier ni au deuxième jet).
Le tableau suivant donne le cheminement pour atteindre le succès en 3 coups :
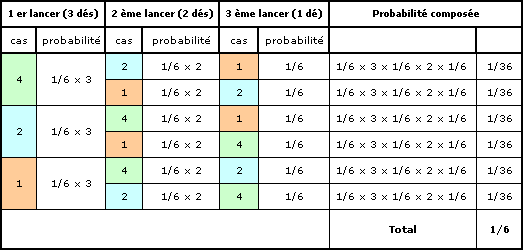
Au premier lancer de dé, il y a 3 cas qui peuvent conduire au succès : obtenir un 4, un 2 ou un 1 avec pour chacun une probabilité de 1/6 x 3 (une chance par dé).
Au deuxième lancer qui ne met plus en oeuvre que 2 dés, il faut partir des 3 cas favorables précédents. Dans le premier cas (4), il n’y a plus que 2 cas favorables (obtention d’un 2 ou d’un 1), avec pour chacun d’eux une probabilité de 1/6 x 2 (une chance par dé).
Au troisième lancer, avec un dé unique, on n’a plus qu’une chance sur 6 d’obtenir le numéro manquant.
Au total, on dénombre 6 voies possibles pour arriver au succès : 4-2-1, 4-1-2, 2-4-1, 2-1-4, 1-4-2 et 1-2-4, avec pour chacun d’eux une probabilité de 1/36, soit globalement une probabilité de succès de 6/36 = 1/6.
Les lecteurs courageux pourront calculer la probabilité de gagner au 421 dans le cas général c’est à dire soit au premier jet, soit au deuxième ou soit au troisième jet !
Nota : jamais un joueur de loto ne jouerait la combinaison 1-2-3-4-5-6 ! Il vous dirait que « ça n’a aucune chance de sortir » ! Mais il joue à chaque fois sa date de naissance de sa femme et la sienne : 14-12-46–4-5-44, une combinaison qui a pourtant exactement la même probabilité de sortir que la combinaison 1-2-3-4-5-6 !!!