1 - Définitions et théorèmes
Définitions
La plupart du temps, il est impossible économiquement d’étudier une population dans son intégralité. On procède alors par un sondage sur une partie seulement de la populaltion. C’est ce que l’on appelle un échantillon.
Echantillonnage aléatoire
Pour qu’un échantillon soit représentatif de la population, il faut que chaque élément de la population ait les mêmes chances d’appartenir à l’échantillon. On parle dans ce cas d’échantillonnage aléatoire.
Echantillonnage exhaustif
Lors de l’échantillonnage, si chaque élément extrait est remis dans la population après relevé de ses caractéristiques, on parle d’échantillonnage non exhaustif.
Dans le cas inverse (on ne remet pas en jeu chaque élément extrait) l’échantillonnage est dit exhaustif.
Remarques :
- Une population finie (dénombrable) sur laquelle on procède à un échantillonnage non exhaustif (on remet les éléments extraits dans la population se comporte comme une population infinie.
- Un échantillonnage exhaustif (on ne remet pas en jeu les éléments extraits) portant sur une population très grande (vis à vis de la taille de l’échantillon) est considérée comme non exhaustif.
Théorèmes
Caractéristiques de la moyenne de l’échantillon
1 – Echantillonnage avec remise (non exhaustif)
Soit une population N dont une propriété présente une moyenne m et un écart-type s. On extrait avec remise en jeu un échantillon aléatoire de taille n parmi cette population.
On démontre que la moyenne de tels échantillons est elle-même une variable aléatoire qui suit approximativement une loi normale ayant les caractéristiques suivantes :
- Moyenne = la moyenne de la population (m),
- Ecart-type :
![]()
On vérifie que plus la taille de l’échantillon (n) est grand plus l’écart-type de la moyenne est faible, ce qui implique que plus l’incertitude sur la moyenne se réduit et se resserre autour de la moyenne.
Dans la pratique, on considère que n est grand au-delà de 30. Dans ce cas, on a n1/2 = 301/2 = 5,48
Si l’on considère la loi normale normée réduite de la population (écart-type = 1), l’écart-type de la moyenne de l’échantillon vaudra : 1/5,48 = 0,18.
La figure suivante compare les distributions de la population initiale et de la moyenne des échantillons :
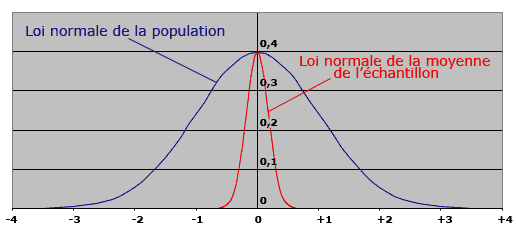
Il s’agit d’un écart-type faible qui donnera une bonne précision dans l’évaluation de la valeur de la moyenne.
2 – Echantillonnage sans remise (exhaustif)
Quand on ne peut remettre les éléments extraits, l’écart-type de la moyenne est obtenu par la formule :
![]()
ATTENTION : dans ce qui précède il ne faut pas confondre l’écart-type (s) de la population étudiée avec l’écart-type de la moyenne calculée sur l’échantillon.
Caractéristiques des proportions
Considérons une population dont une certaine proportion (p) d’éléments possède une certaine propriété. On aimerait connaître ce qu’il advient de cette proportion dans l’échantillon prélévé.
On démontre que dans tout échantillon aléatoire de taille suffisante avec remise en jeu, la proportion d’éléments possédant une propriété suit une loi normale ayant les caractéristiques suivantes :
- Moyenne : la proportion initiale,
- Ecart-type :
![]()
Par exemple, imaginons un échantillon de 100 personnes parmi une population dont 10 % mesurent plus de 1m80, on obtient un écart-type de la proportion dans l’échantillon égal à: 0,03. Cela signifie que dans une plage à ± 1 sigma autour de la proportion moyenne, c’est à dire dans l’intervalle [0,07 ;0,13], on trouvera 68 % des valeurs de la proportion.
On note également que la précision augmente quand la taille de l’échantillon augmente mais en proportion de la racine de cette taille. cela signifie que pour doubler la précision il faut multiplier la taille de l’échantillon par 4 !
